Introduction
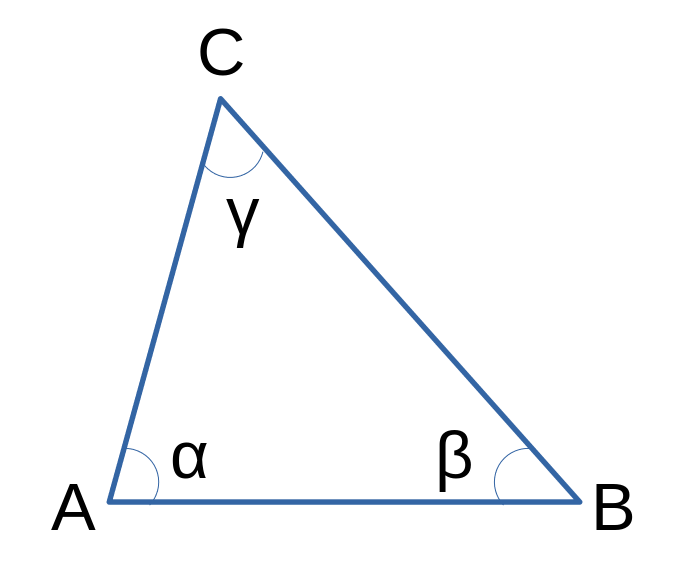Je me suis toujours demandé pourquoi la somme des angles d’un triangle était constante et égale à 180°. Comment parvient-on à une telle affirmation ?
L’histoire raconte que Blaise Pascal (mathématicien français du XVII ième siècle) aurait démontré cette proposition d’Euclide à l’âge de 11 ans … cela m’a toujours fasciné.
Comment un enfant de seulement 11 ans a-t-il bien pu parvenir à ce résultat ?!?
Bizarrement, une réponse m’est venue un jour sous la douche, alors que j’y pensais sans vraiment y réfléchir 🙂
Le raisonnement est géométrique et plutôt intuitif. Les figures se sont formées dans mon esprit et la solution m’est apparue d’un coup comme une évidence.
2 triangles valent mieux qu’1
Reprenons la figure présentée dans l’introduction et dupliquons la.
Déplaçons ensuite ce 2ième triange de façon à ce que les point B et A’ des 2 trianges coïncident (AB restant // à A’B’).
Nous obtenons la figure ci-dessus.
Puisque les triangles sont identiques, leurs angles sont également égaux (α, β et γ).
De la même façon, entre les 2 triangles, les côtés restent deux à deux parallèles et de mêmes longueurs :
- AB // A’B’ (par construction) et [AB] = [A’B’] donc
- AC // A’C’ et [AC] = [A’C’]
- CB // C’B’ et [CB] = [C’B’]
3 triangles valent mieux que 2
Poursuivons le délire de la multiplication des triangles. Ce coup-ci, nous allons appliquer une homothétie de rapport -1 et de centre C :
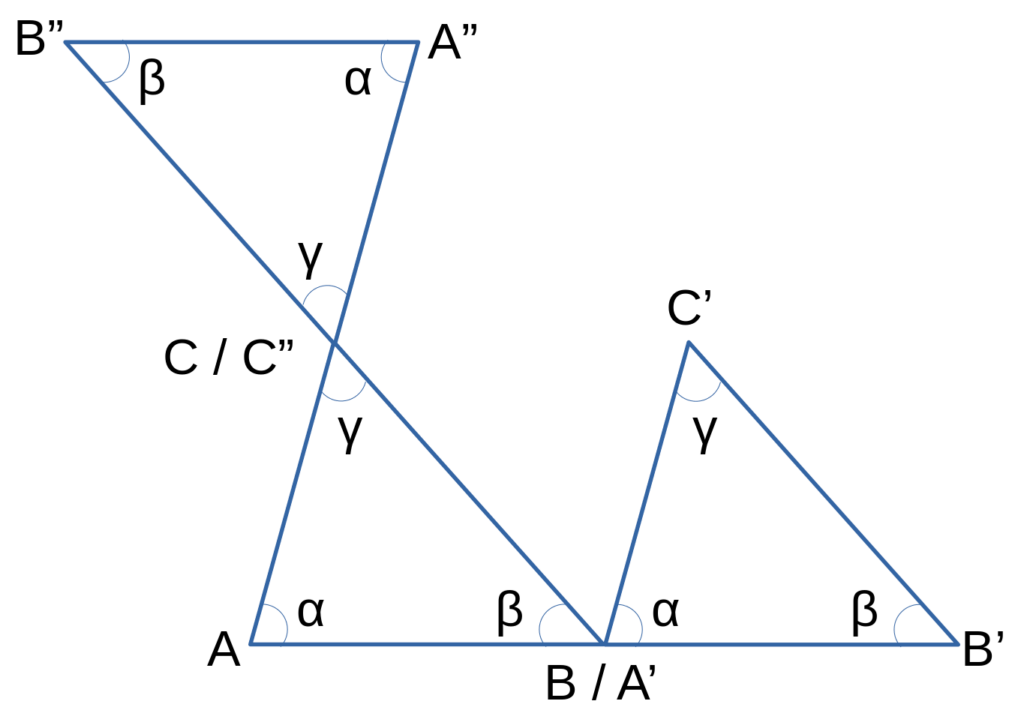
Le triangle A”B”C” est en tout point identique à ses 2 frères jumeaux (des triplés en somme). Il est simplement “inversé”.
Nous pouvons assez intuitivement en déduire les relations suivantes :
- AB // A’B’ // A”B” et [AB] = [A’B’] = [A”B”]
- AC // A’C’ // A”C” et [AC] = [A’C’] = [A”C”]
- CB // C’B’ // C”B” et [CB] = [C’B’] = [C”B”]
La solution par translation
Vous ne vous en êtes peut être pas rendu compte, mais la réponse est déjà sous vos yeux.
Tel un tangram, il ne reste qu’à effectuer une translation du triangle A”B”C” suivant l’axe CB de façon à ce que le sommet C” coïncide avec les sommets B et A’ … la réponse en image :
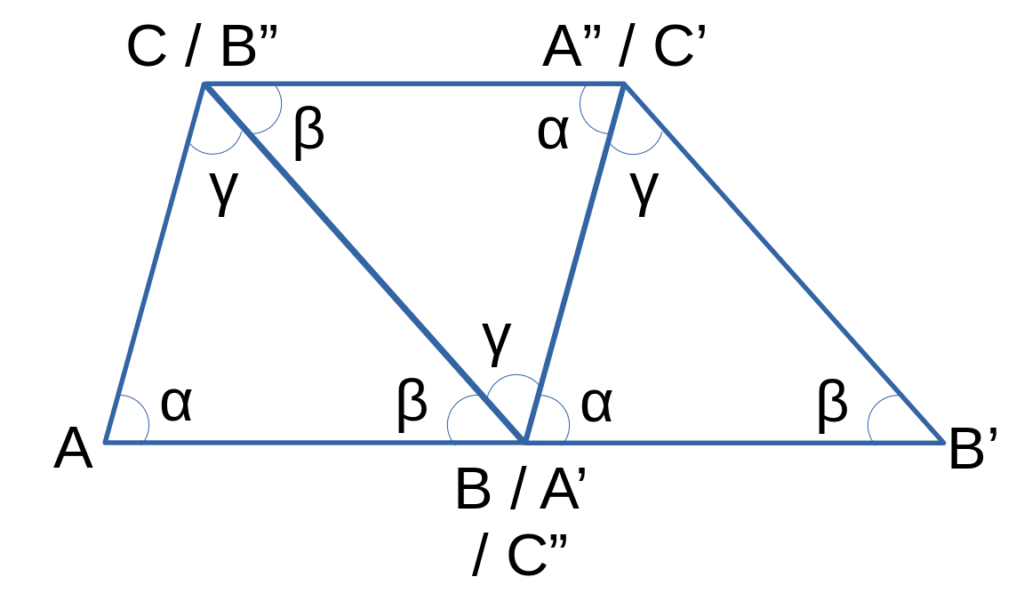
Dans le triangle ABC, le sommet B forme un angle connu β. De la même façon, dans le triangle A’B’C’, le sommet A’ a pour valeur d’angle α. Par construction AB et A’B’ sont parallèles (et superposées).
Reste la question de l’angle formé en B par CBC’.
Puisque BC // B”C” et que BC’ (ou A’C)’ // A”C”, la valeur de l’angle manquant est donc bien celle du sommet C” de B”C”A”, c’est à dire γ.
Comme on le voit au point B (ou A’ ou C”), l’ensemble des angles α, β et γ forme un angle plat.
Autrement dit :
α + β + γ = 180°
CQFD
Pourquoi faire simple ?
Ce qui est amusant dans cette histoire, c’est que je sois parvenu à une solution par moi-même en partant de rien (et sous la douche) 🙂
Depuis, j’ai regardé sur internet quelle démonstration était en général proposée pour ce problème …
Oui, on pourrait se poser la question de savoir pourquoi je n’ai pas commencé par là ?? La satisfaction de trouver soi-même, voilà pourquoi 😀
Bien sûr, il existe une approche beaucoup plus simple qui se base sur la notion d’angles alternes-internes.
Un petit schéma vaut mieux qu’un long discours :
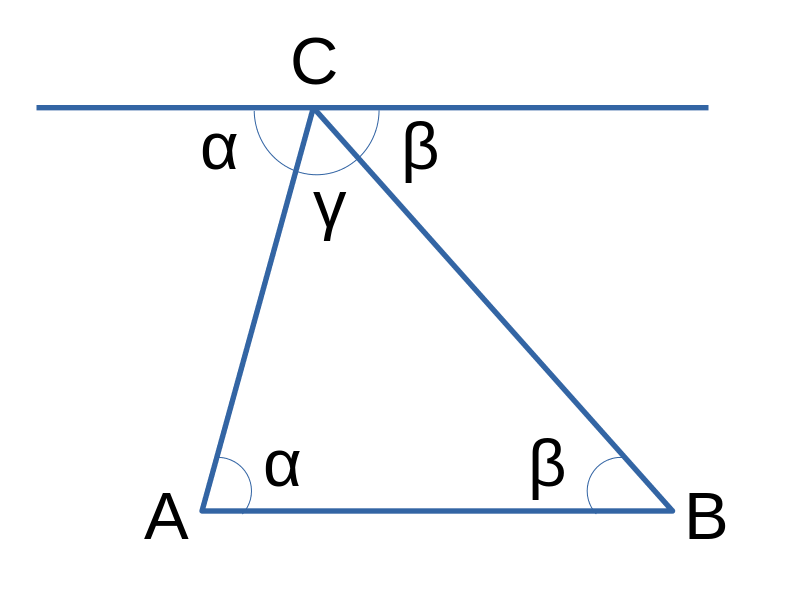
Si on trace la droite parallèle à (AB) passant par C, d’après les propriétés des angles alternes-internes, on retrouve tout de suite les angles α et β de part et d’autre de l’angle γ.
L’angle plat est ainsi immédiatement visible.
En fait, j’arrive au même résultat (puisqu’on retrouve aussi les angles alternes-internes dans ma construction), mais juste de façon plus alambiquée 😀
Et voici une démonstration détaillée avec un sympathique accent québecois: